勝率50%のEAでもロット数調整だけでリカバリーファクターを大幅に改善させる戦略（分解モンテカルロ法）

この記事では、勝率50%のEAでも、分解モンテカルロ法でロット数を調整すればリカバリーファクターを大幅に改善させることが可能かどうかを検証し、その結果を考察します。

以下の流れでお送りしますので、是非最後までご覧ください。

10年間で勝率が50%程度のEAを用意します。
ロット数を調整する方法をいくつか試します。
リカバリーファクターがどの程度改善するか確認します。

リカバリーファクターとは

リカバリーファクターは、EA（Expert Advisor）のバックテストで使用される指標でトレード戦略のパフォーマンスを評価するための指標の一つです。獲得した利益とドローダウン（一時的な損失）の比率を示しており、計算式は以下の通りです。

リカバリーファクター = 総損益 / 最大ドローダウン

リカバリーファクターが高いほど、そのEA（トレード戦略）は効率的に利益を上げる能力があるとされています。個々のトレーダーのリスク許容度によりますが、一般的には、リカバリーファクターが2.00以上の戦略は良好とされ、3.00以上であれば優れていると評価されます。

勝率50%のEA（ベースモデル）

まずは、勝率が50%程度のEAを用意します。

トレード戦略

このEA（ベースモデル）のトレード戦略は以下の通りです。（非ナンピン型EAです。）

MAとDMIというテクニカル指標を使って売買タイミングを判定します。
利確幅とロスカット幅はATRを基準に定めます。
利確幅とロスカット幅はほぼ同じにしていますが、勝率50%でも損益がプラスになるように少しだけ利確幅のほうが大きくなるように設定しています。
buyポジションおよびsellポジションそれぞれで同時に最大4つまでポジションをとりますが、それぞれのポジションは独立に利確とロスカットを行います。（ナンピンではなく、4つのトレード戦略が並行して稼働するイメージです。）

この記事の本題はEAのロジック部分ではないので、より詳細は省略します。ロジックに関しては、以下の記事をご覧ください。

ADM-EA（分解モンテカルロ法）のロジック詳細解説

この記事では、ADM-EA（分解モンテカルロ法）のロジックを解説していきます。EAを作成するスキルがある程度あれば、この記事を読むだけで同様のEAを作成することは可能だと思いますので、是非オリジナルEAの作成にチャレンジしてみてください。A

このベースモデルのパフォーマンスは以下の通りです。

バックテスト設定

銘柄:

GBPJPY

期間:

10年間 (2013.01.01 – 2022.12.31)

通貨:

JPY

初期証拠金:

100万円

ロット数:

0.01固定

バックテスト結果

パフォーマンス分析

10年間で総損益は106,345円です。証拠金最大ドローダウンは93,373円です。
取引数は6,154回、勝率は50.34%です。
プロフィットファクターは1.04、リカバリーファクターは1.14です。

グラフをご覧になって視覚的に分かるように、10年間で勝率が約50%ですので、勝ち続ける時期もあれば負け続ける時期もあり、期間の切り取り方によってはパフォーマンスが50%以下になってしまうこともあると思います。このグラフ形状をロット数調整だけで可能な限り良いものにしてみようというのが今回の試みです。

ロット数の設定

ベースモデルでは、ロット数は0.01で固定とします。つまり、バックテストでは取引数が6,154となっていますが、この全ての取引はロット数0.01で行われた結果です。

以降の戦略では、このロット数の設定部分のみを変更してバックテスト結果がどのように変わるのかを検証していきます。

マーチンゲール法の導入（ロット数制限なし）

まずは、ロット数設定にマーチンゲール法を導入することについて検証します。

マーチンゲール法は、ギャンブルやトレーディング戦略で使用される手法で、損失が発生した場合に次の賭けやトレードでリスクを増やすことで損失を回復しようとするものです。具体的には、負ける度に賭け金やポジションサイズ（ロット数）を増加させます。いずれ訪れる勝ちのタイミングで、それまでの損失を取り戻して利益を上げることを目指します。

ここでは、1つのエントリーは必ず利確またはロスカットのどちらかになり、利確することを勝ち、ロスカットすることを負け、と捉えてマーチンゲール法を適用します。

ロット数決定ルールの確認

負けたらロット数を2倍にするマーチンゲール法では、連続してロスカットが発生するたびにポジションサイズ（ロット数）を2倍に増やします。最初のロット数が0.01の場合、以下のようなシナリオが考えられます。

1回目：ロット数 0.01（ロスカット）
2回目：ロット数 0.02（ロスカット）
3回目：ロット数 0.04（ロスカット）
4回目：ロット数 0.08（ロスカット）
5回目：ロット数 0.16（ロスカット）
6回目：ロット数 0.32（利確）

この例では、6回目のトレードで利確するまでに5回連続でロスカットが発生しています。負け取引の総ロット数は0.31です。しかし、6回目のロット数が0.32ですので、利確した場合はそれまでのロスカットによる損失を取り戻し、ロット数0.01に相当する利益を上げることができます。

また、実際に確かめてみると分かりますが、何回目のトレードで勝ち（利確）になったとしても、最終的な利益はロット数0.01に相当します。以上が、マーチン倍率が2倍のマーチンゲール法の例です。

なお、一度利確をしたら、その次のトレードは0.01から再び始めるのがルールです。連敗し続ければ無限にロット数が増え続けて行くのでリスクが高いですが、まずはロット数の制限は設けずに検証することにします。

バックテスト設定

銘柄:

GBPJPY

期間:

10年間 (2013.01.01 – 2022.12.31)

通貨:

JPY

初期証拠金:

1億円

ロット数:

マーチンゲール法（ロット数制限なし）

ロット数制限なしのマーチンゲール法では、状況によっては必要証拠金が莫大になってしまうので、ロット数が増え続けてもトレードが止まらないように、初期証拠金を100倍の1億円にして検証します。

バックテスト結果

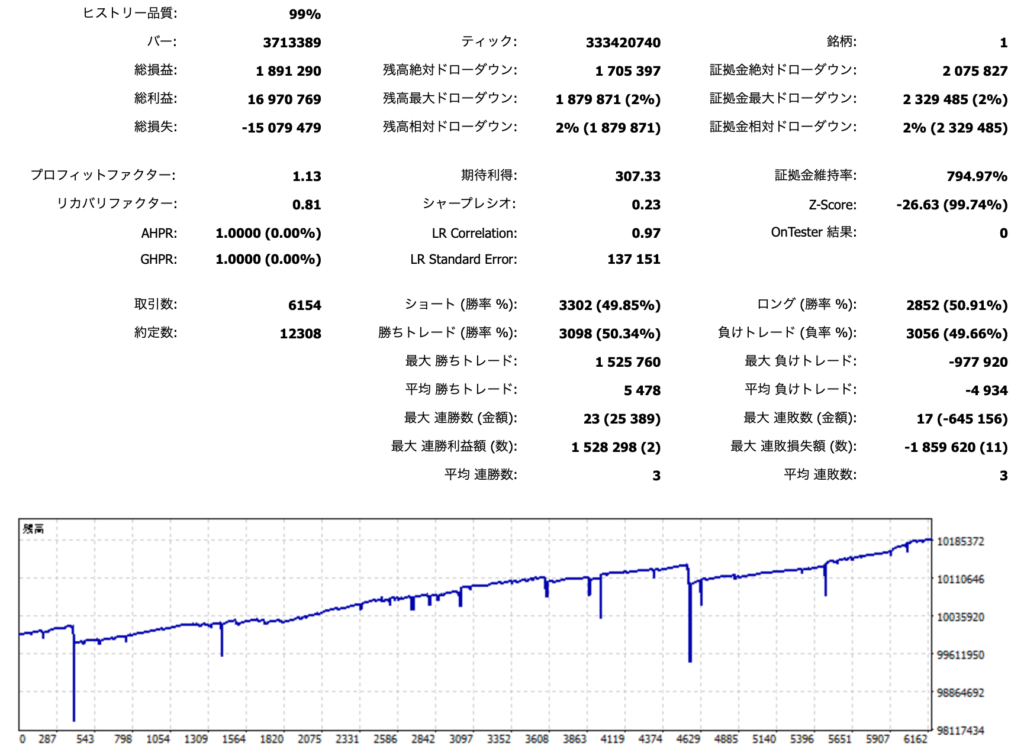
パフォーマンス分析

10年間で総損益は1,891,290円です。証拠金最大ドローダウンは2,329,485円です。
取引数は6,154回、勝率は50.34%です。（ベースモデルと全く同じ）
プロフィットファクターは1.13、リカバリーファクターは0.81です。

10年間で189万円の利益が上げられるのですが、最大ドローダウンは232万円ということで、リカバリーファクターが1を下回ってしまっています。これはつまり、利益の絶対額は大きくなっていますが、破綻しないために必要な証拠金の額も大きくなって資金効率が悪くなっているということです。

また、ここで確認しておいていただきたいのが、取引数と勝率が先のベースモデルと全く同じになっていることです。取引タイミングは全く同じでもロット数の戦略を変えるだけで結果が大きく異なってくるということがよく分かるかと思います。

なお、このようなグラフはマーチンゲール法を取り入れているEAではよくある形状です。無限に資金があれば必ず損失を取り返すという戦略なので、このような右肩上がりの損益グラフになりやすいです。

グラフをよく見れば、厳密にはその瞬間に損失を取り返せていないポイントがあることがわかると思います。これは、1回の取引による利確幅やロスカット幅をATRに連動させて決定している影響です。各トレードタイミングのATRに差があると、利確幅やロスカット幅が毎回異なってくるために起こる現象です。

マーチンゲール法の導入（ロット数制限あり）

続いて、マーチンゲール法にロット数制限を加えたモデルで検討してみます。

バックテスト設定

銘柄:

GBPJPY

期間:

10年間 (2013.01.01 – 2022.12.31)

通貨:

JPY

初期証拠金:

100万円

ロット数:

マーチンゲール法（最大ロット数 0.30）

ここでは初期証拠金は100万円に戻して、最大ロット数は0.30とします。

最大ロット数の設定は、マーチンゲールによってロット数を増やし続ける中で、そのロット数を超えてしまった場合は0.01に戻る。という目的で使用します。例えば先ほどの例では、6回目のトレードのロット数は0.32になりますが、最大ロット数である0.30を超えているので、0.01に戻します。つまり、6回目のトレードで勝ってもそれまでの損失を取り返すことは出来ません。言い換えれば、5連敗した場合は損失を受け入れる（取り返すことを諦める）という戦略です。

バックテスト結果

パフォーマンス分析

10年間で総損益は152,477円です。証拠金最大ドローダウンは273,116円です。
取引数は6,154回、勝率は50.34%です。（ベースモデルと全く同じ）
プロフィットファクターは1.02、リカバリーファクターは0.56です。

ロット数制限を設けたことで、利益もドローダウンも10分の1程度になっています。ただし、リカバリーファクターはさらに悪化してしまいました。最大ロット数の制限を0.30（5連敗）と設定したところがそこまで効果的に機能していないことが分かります。勝率50%でも、5連敗くらいはわりと頻繁に起きるという結果でしょう。

確率を計算してみると、50%（1/2）の負けを5回連続引くということで3%程度ですが、6,000回も取引していれば180回は起こる頻度なので、そんなにレアな印象は受けません。

以上、マーチンゲール法でリカバリーファクターを向上させるのはなかなか難しいことが分かりました。

分解モンテカルロ法の導入（ロット数制限あり）

続いて、分解モンテカルロ法について検証します。

マーチンゲール法と同様にギャンブルの領域において利用される賭け方の1つにモンテカルロ法というものが存在します。そのモンテカルロ法の欠点を改善した手法が分解モンテカルロ法です。以下の記事を参考にさせていただきましたので、詳細は考案者の方のサイトでご確認ください。

分解モンテカルロ法の詳細解説｜Chisiki

原案者について元からカジノのベットシステムとしてモンテカルロ法は存在していたのですが様々なデメリットがあり、それを改良した分解モンテカルロ法をict119さんが考案しシュミレーションなどをして解説していたのですが執筆時点(20年5月28日）でご本人のサイトにアクセスできなくなっており、このとても有用なベットシステムを...

モンテカルロ法（賭け）の欠点＆改良手法の提案(c++)

はじめに ※目次用の記事：ギャンブルの賭け方の種類をまとめてみたモンテカルロ法と聞くと、多くの方は、乱数を用いて数値解析する手法としてのモンテカルロシミュレーションをイメージされる人は多いと思うが、この記事で扱うのは、ギャンブルの領域

EAに適用するということを意識した上で、この分解モンテカルロ法の特徴を簡単にまとめると以下の通りです。

数列がリセットされると最終的な収支はプラスになる。
ロット数の増大が緩やかで、損失は時間をかけて緩やかに回収する。
以上より、リスクを軽減させたマーチンゲール法の改良版ともいえる。

ロット数決定ルールの確認

数列のルール

初めに[0, 1]という数列を準備する。
数列の左端と右端を足し合わせた数だけ賭ける。（最初は0+1=1）
負けた場合：賭け金額を数列の右端に加える
勝った場合：数列の一番右端と一番左端を消す
数列が完全に消えた場合は、数列をリセット。数列は[0, 1]から再びスタートする。
数列が1つ残った場合は、数字をなるべく均等に分解する。数列は、分解した2つの数字を並べた数列を使用する。
例：数字分解時は、小さい数字を左に、大きい数字を右に書く。
「5→[2, 3]」、「8→[4, 4]」、「11→[5, 6]」

ロット数決定ルール

上記数列のルールから導出された賭ける数値の0.01倍のロット数をトレードに使用します。

ルールに従い、3回負けて、1回勝ち、4回負けて、4回勝った場合のロット数を計算してみましょう。（少し長いですが具体例で見た方がルールがわかりやすいのでお付き合いください。）

1回目
- 数列：[0, 1]（最初の数列）
- ロット数：0.01（0+1=1）
- 結果：ロスカット
2回目
- 数列：[0, 1, 1] （前回負けたので1を右端に追加）
- ロット数：0.01（0+1=1）
- 結果：ロスカット
3回目
- 数列：[0, 1, 1, 1] （前回負けたので1を右端に追加）
- ロット数：0.01（0+1=1）
- 結果：ロスカット
4回目
- 数列：[0, 1, 1, 1, 1] （前回負けたので1を右端に追加）
- ロット数：0.01（0+1=1）
- 結果：利確
5回目
- 数列：[1, 1, 1] （前回勝ったので左端と右端の数字を消す）
- ロット数：0.02（1+1=2）
- 結果：ロスカット
6回目
- 数列：[1, 1, 1, 2] （前回負けたので2を右端に追加）
- ロット数：0.03（1+2=3）
- 結果：ロスカット
7回目
- 数列：[1, 1, 1, 2, 3] （前回負けたので3を右端に追加）
- ロット数：0.04（1+3=4）
- 結果：ロスカット
8回目
- 数列：[1, 1, 1, 2, 3, 4] （前回負けたので4を右端に追加）
- ロット数：0.05（1+4=5）
- 結果：ロスカット
9回目
- 数列：[1, 1, 1, 2, 3, 4, 5] （前回負けたので5を右端に追加）
- ロット数：0.06（1+5=6）
- 結果：利確
10回目
- 数列：[1, 1, 2, 3, 4] （前回勝ったので左端と右端の数字を消す）
- ロット数：0.05（1+4=5）
- 結果：利確
11回目
- 数列：[1, 2, 3] （前回勝ったので左端と右端の数字を消す）
- ロット数：0.04（1+3=4）
- 結果：利確
12回目
- 数列：[2] （前回勝ったので左端と右端の数字を消す）
- 数列：[1, 1]（数字が1つになったので2を分解）
- ロット数：0.02（1+1=2）
- 結果：利確（数字が全て消えたので終了）

改めて、表形式で結果をまとめると以下の通りです。

回目	数列	ロット数	結果
1	[0, 1]	0.01	ロスカット
2	[0, 1, 1]	0.01	ロスカット
3	[0, 1, 1, 1]	0.01	ロスカット
4	[0, 1, 1, 1, 1]	0.01	利確
5	[1, 1, 1]	0.02	ロスカット
6	[1, 1, 1, 2]	0.03	ロスカット
7	[1, 1, 1, 2, 3]	0.04	ロスカット
8	[1, 1, 1, 2, 3, 4]	0.05	ロスカット
9	[1, 1, 1, 2, 3, 4, 5]	0.06	利確
10	[1, 1, 2, 3, 4]	0.05	利確
11	[1, 2, 3]	0.04	利確
12	[1, 1]	0.02	利確

以上より、ロスカットの総ロット数は0.17で、利確の総ロット数は0.18です。つまり、最終的にロット数0.01の利益を確保してそのセットを終了することが可能ということです。

一連の流れでは、負けてもロット数が増えない、または0.01ずつしか増えてないということがわかります。マーチンゲール法であれば倍々にロット数が増えるところ、分解モンテカルロ法ではロット数の増加が緩やかです。また、マーチンゲール法であれば1回の勝ちで1セットが終了するところ、分解モンテカルロ法の場合は5回勝ってようやく1セット終了という形で、損失を回収する過程も緩やかです。